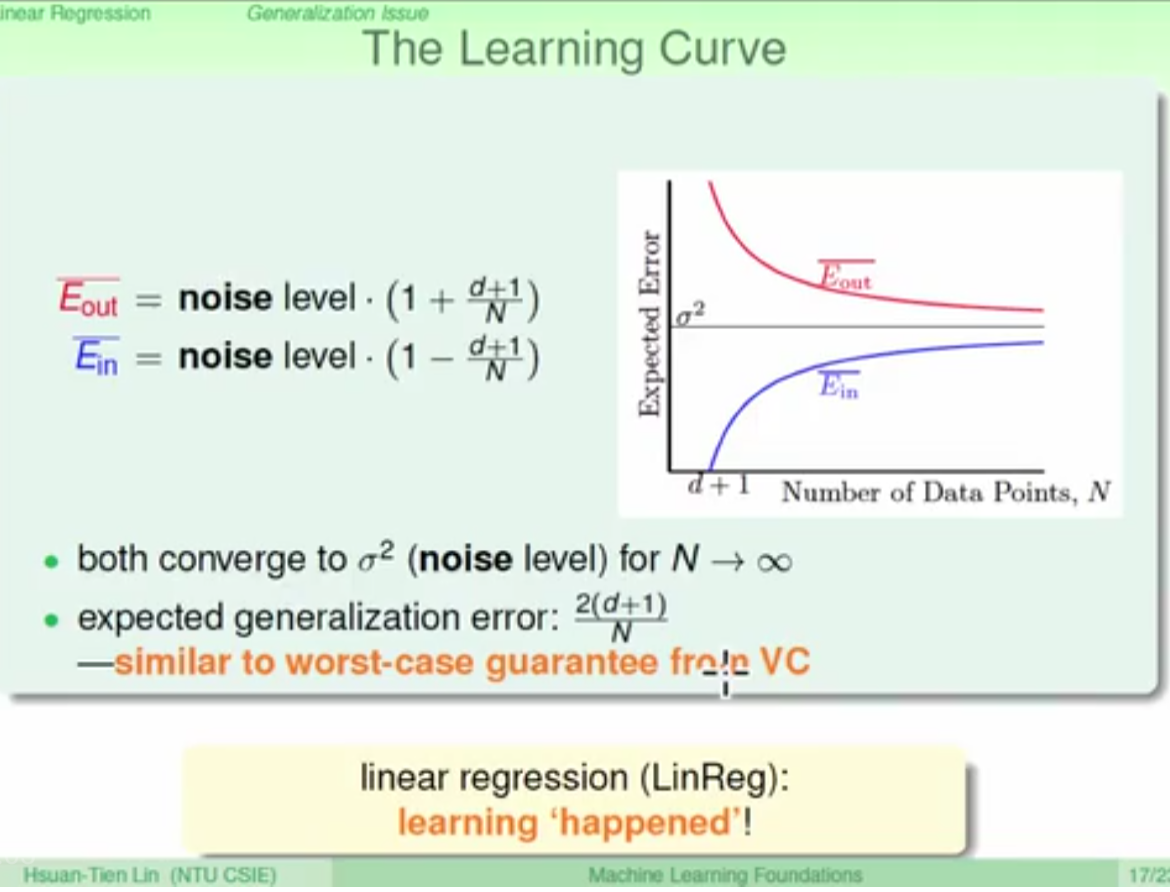
Linear regression
during linear regression, both Ein and Eout converge to sigma square, so the expected error( square error) between them is show in the pic.
d: vc dimension
N: Number of data points
logistic regression
Error definition
the output of logistic regression is generated by sigmoid function
the logistic regression error is defined by maximizing the likelihood the h equal f, which is called crosss entropy error. this error is related to w, xn and yn


this is the mathmatical form of cross entropy error for calculation
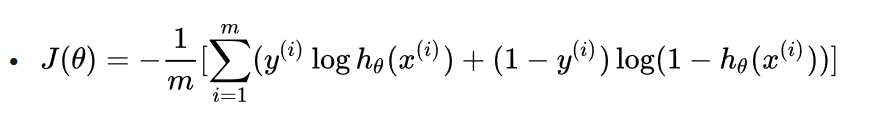
Gradient decent and learning rate
the optimal gradient descent direction is opposite direction of Delta-Ein

purple niu is teh learning rate

the training process is described in the chart

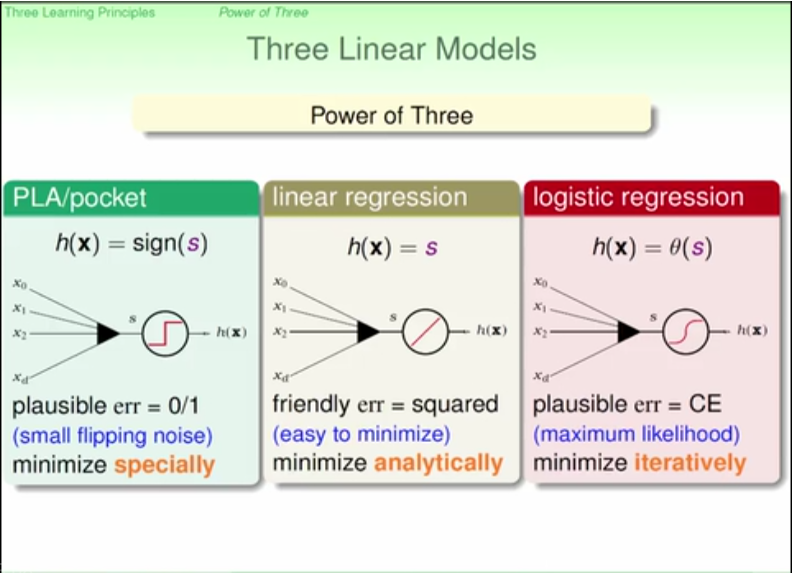
Linear model
advantages and disadvantages
demenstration of advantages and disadvantages between threee linear models

optimization process
what means stochastic gradient descent??

SGD logistic regression can be seen as a softed PLA
stop criterien during training:
*iteration times
niu (learning rate )is set as 0.1(experience value)

multiclass classification
two methods to deal with multiclass classification
- OVA(one versus all)[not recommended, not clearly seperatable]
- OVO(one versus one )


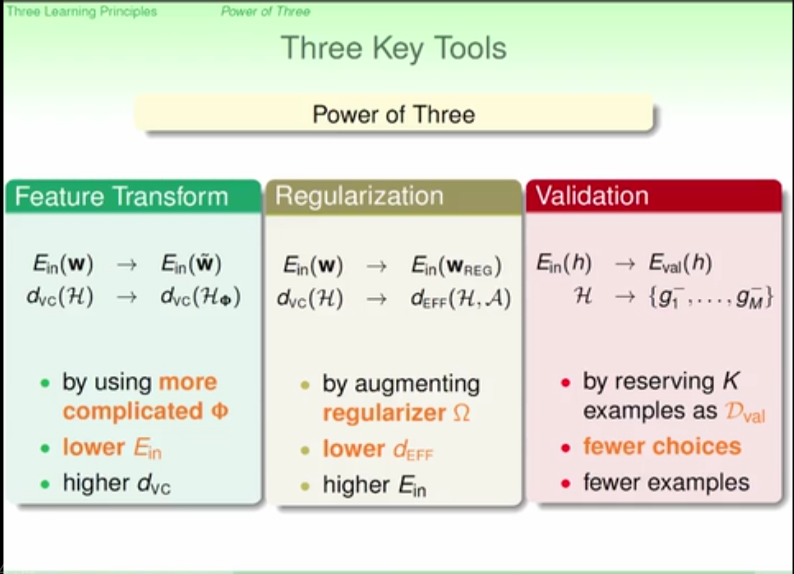
nonlinear transformation
the principle to deal with nonlinear problem is to transform the data from nonlinear space to linear space, and use linear model to deal with it. However this will lead to more complex model, so there are some parameters( C, lambda) to restrict the complexity of the model (regularization???)


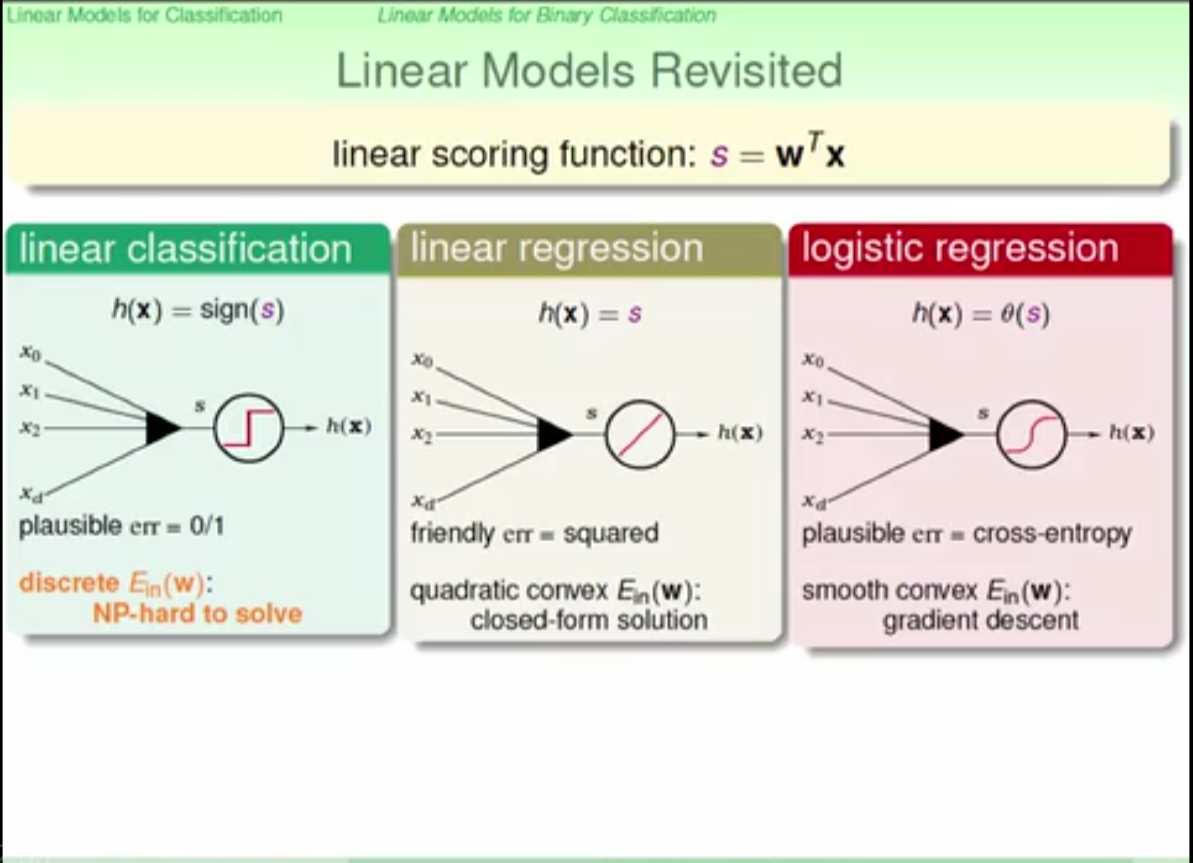
overfitting
use more complex model is not good expecially when number of data points is small
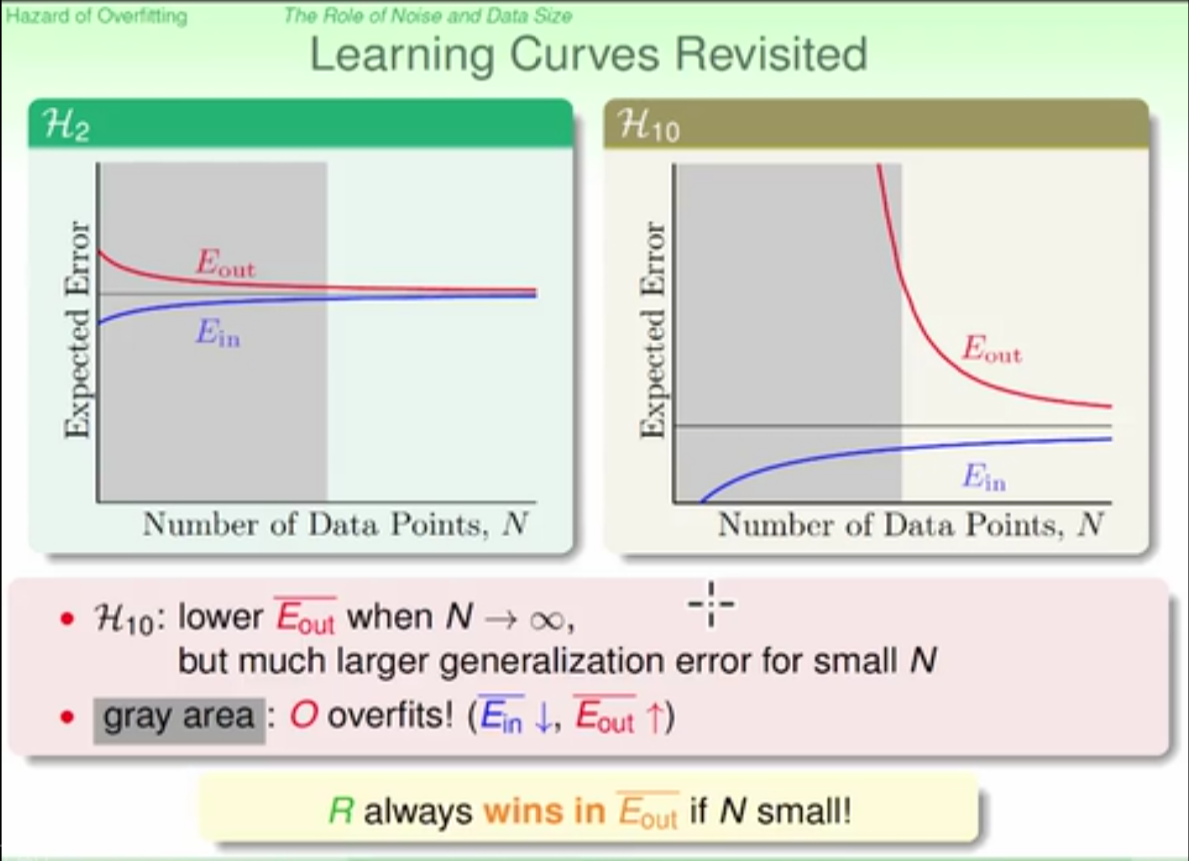
four reasons leading to oversfitting:
- data size
- stochastic noise
- deterministic noise
- excessive power (model complexity)
suggested ways to avoid overfitting:
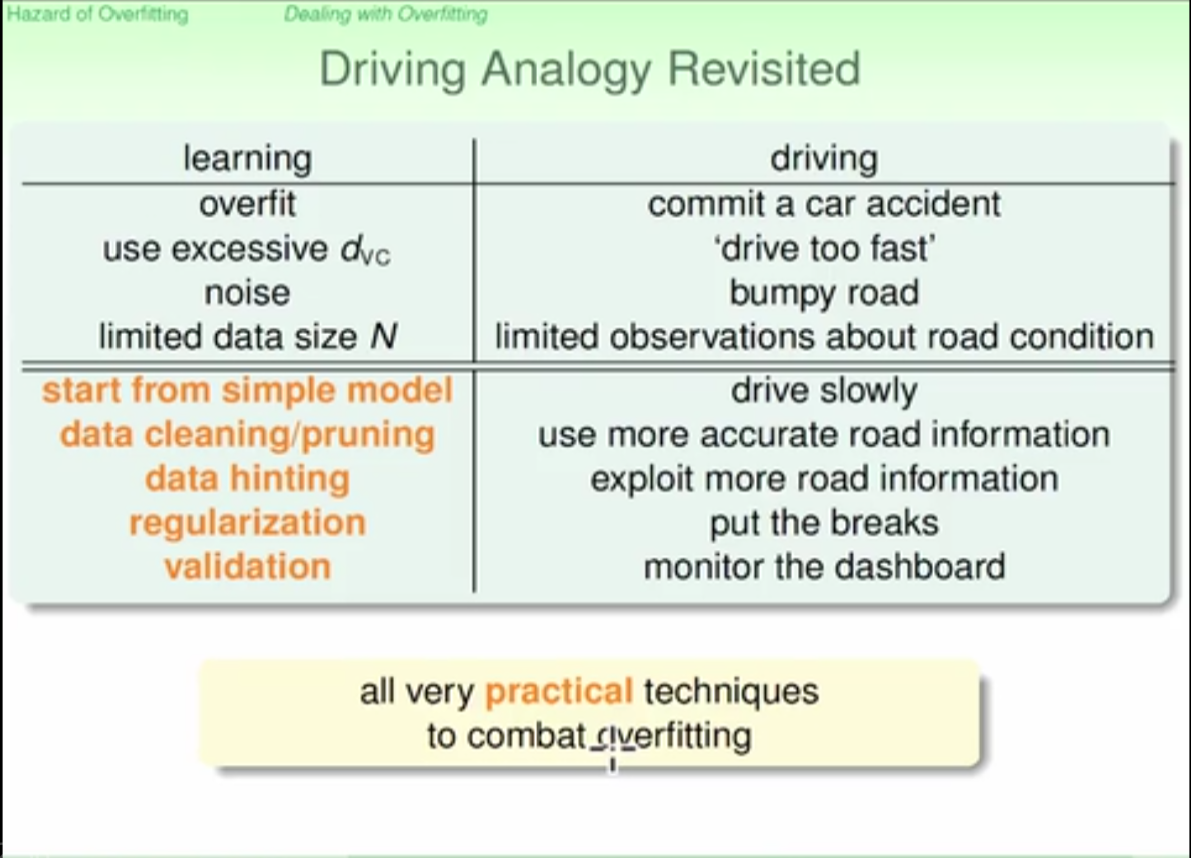

regularization
loosing and softing the constraints to deal with the nonlinear problem


augemented error definition and regularizer definition
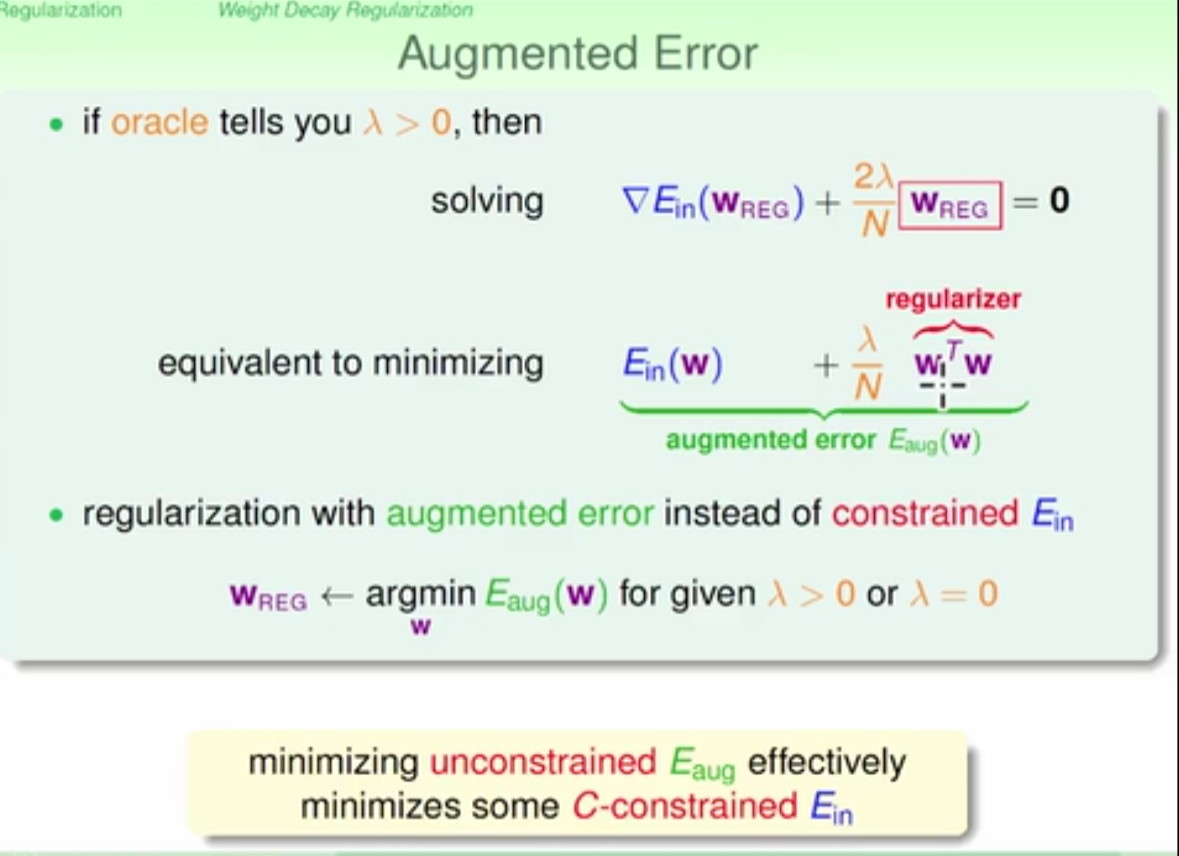
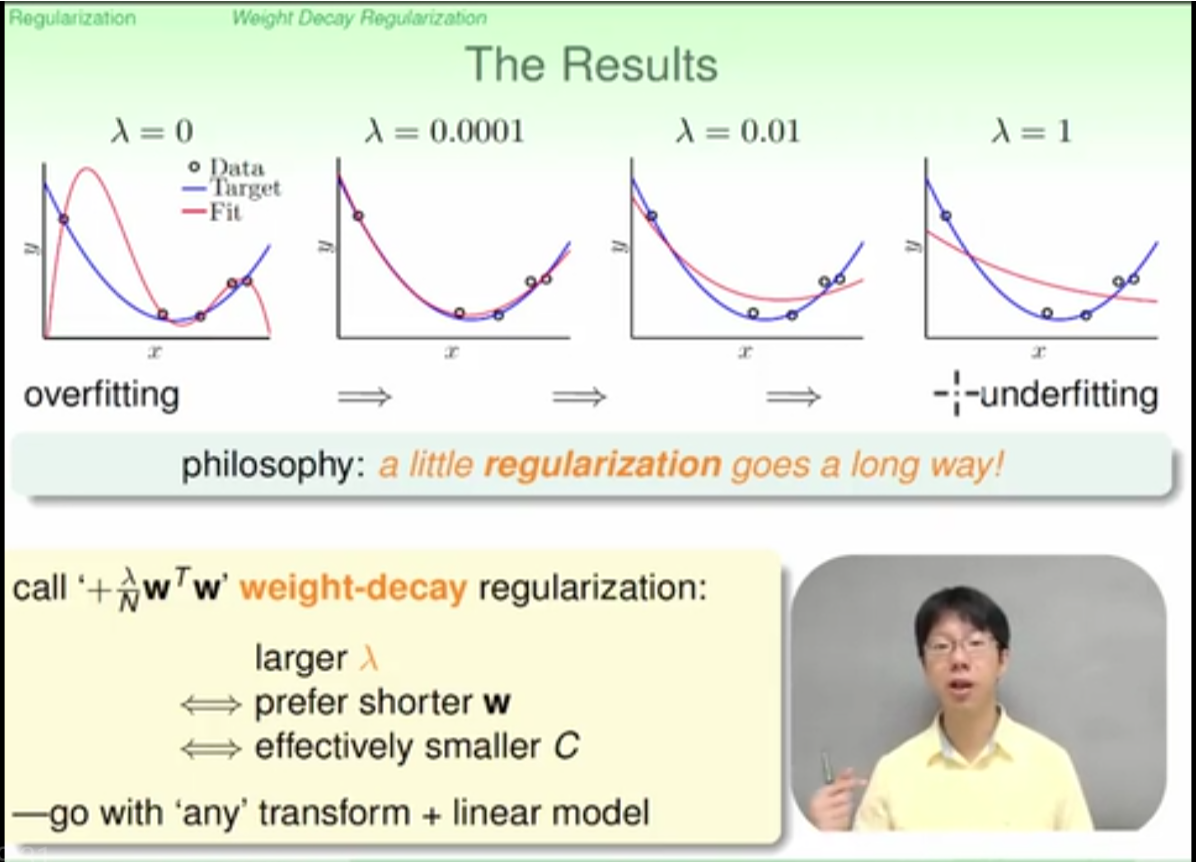
regularization prefers smaller lambda and smaller w step during training
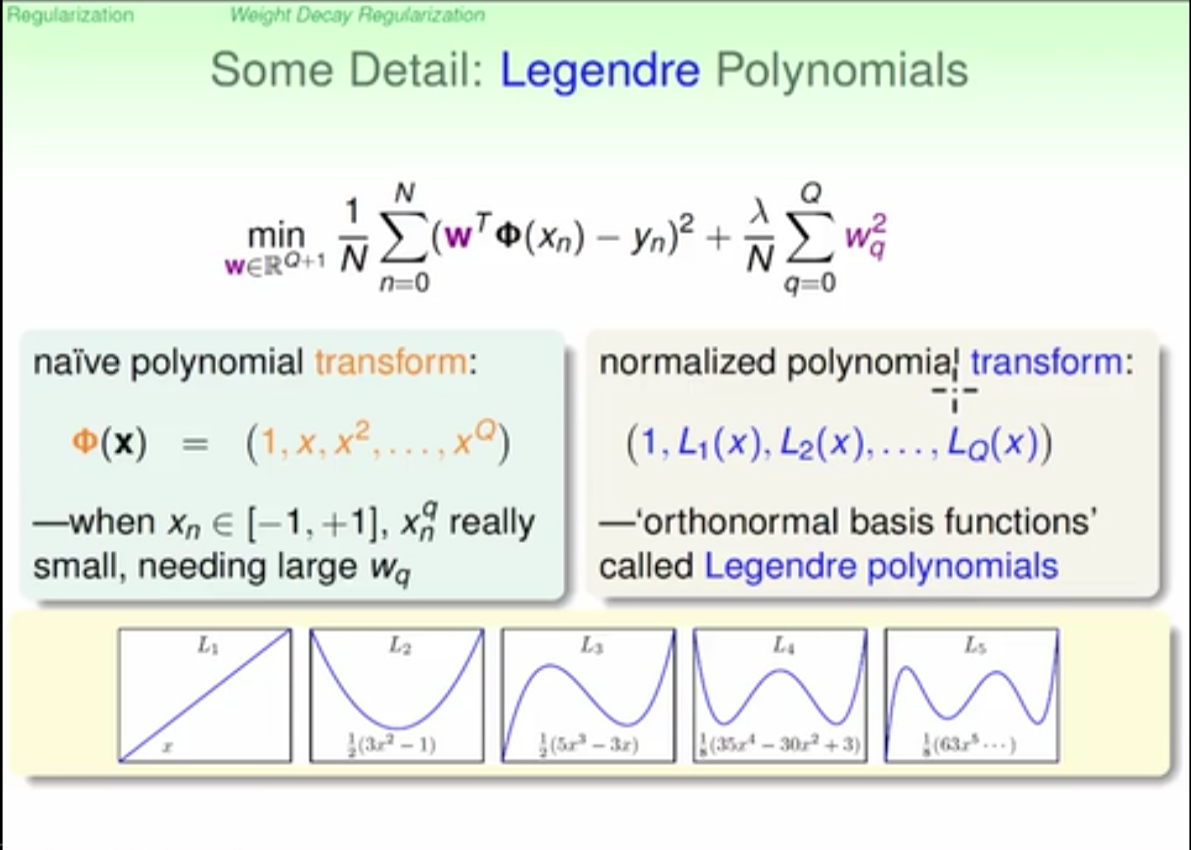
more effective transformation using legendre polynomials than naive polynomials
regularization confines to VC guarante with somehow enlarged error range
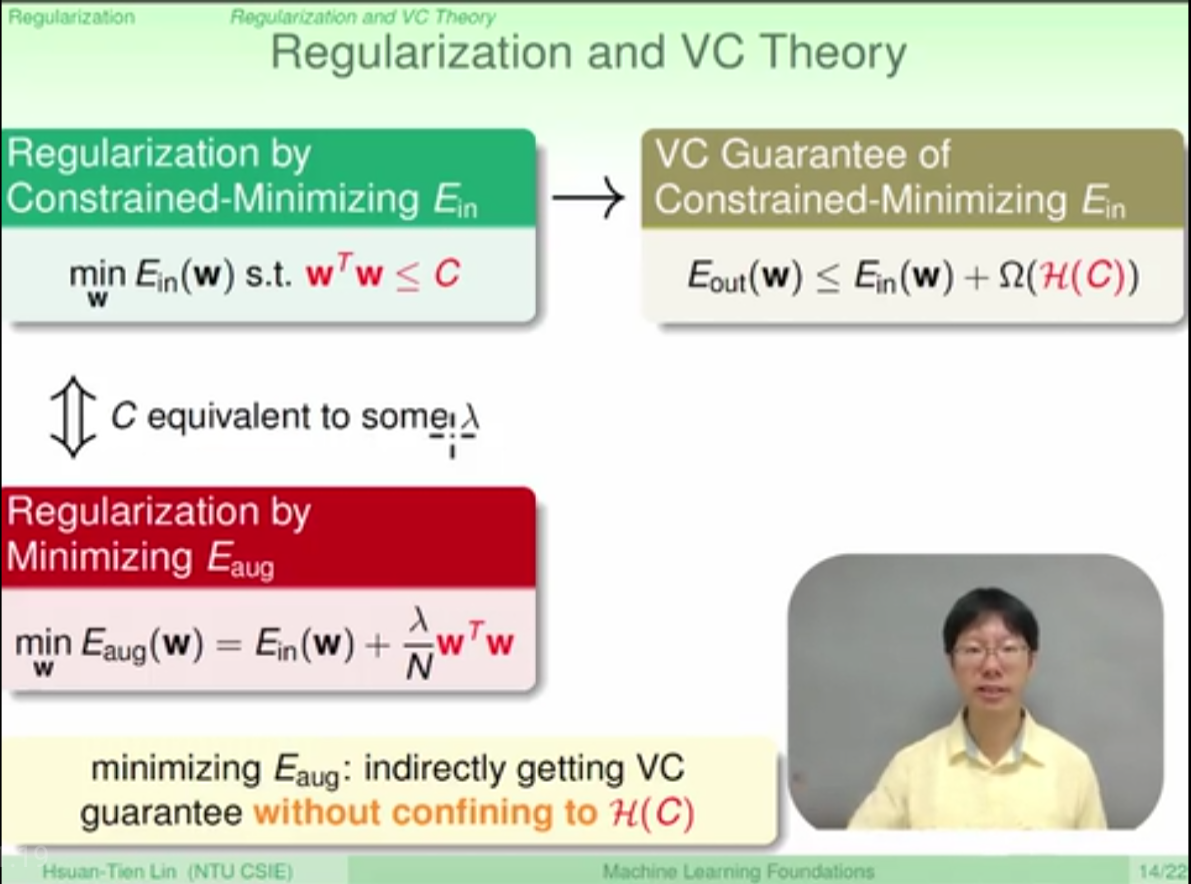
the model complexity is reduced due to regularization

if lambda increases, the effective vc dimension is reduced

principles to design regularizer:
- target dependent
- plausible
- friendly

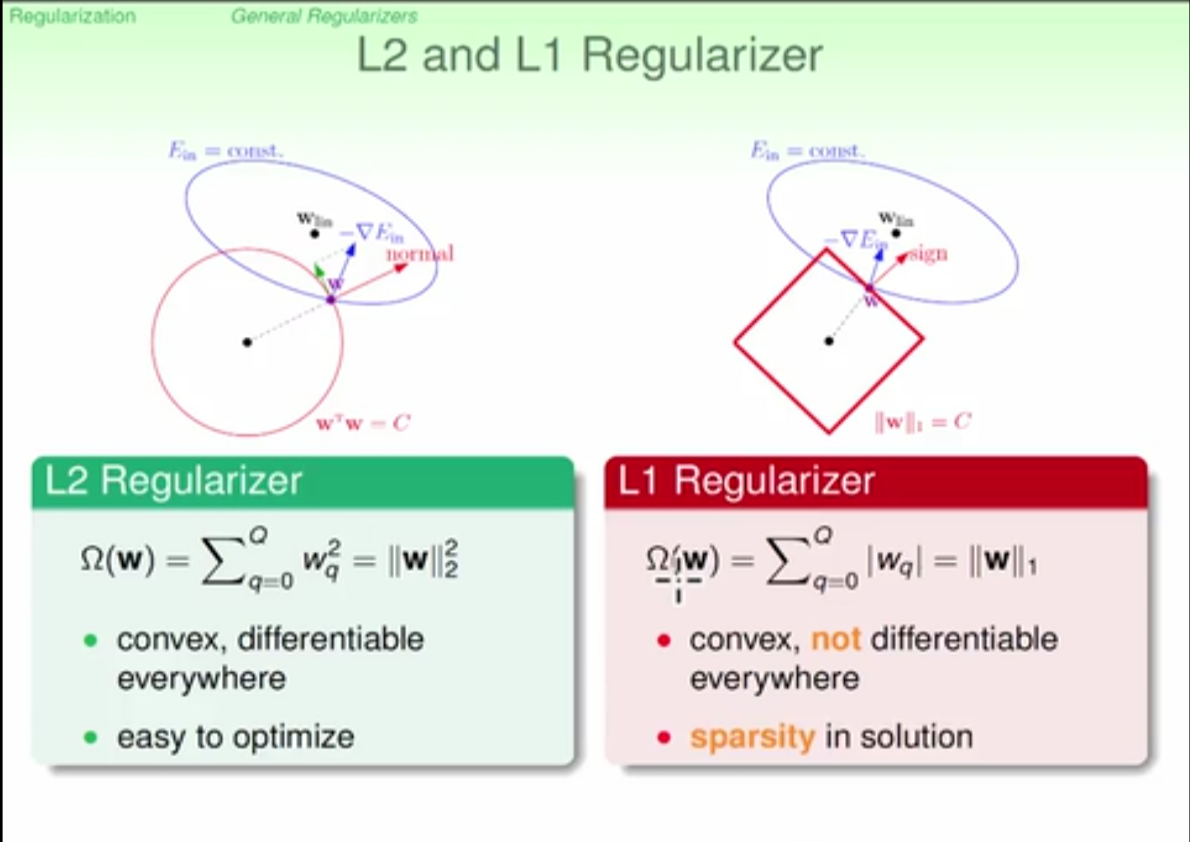
L1 regularizer: time-saving in caculation, solution is sparse but not optimal
L2 regularizer: easy to optimize, precise in solution
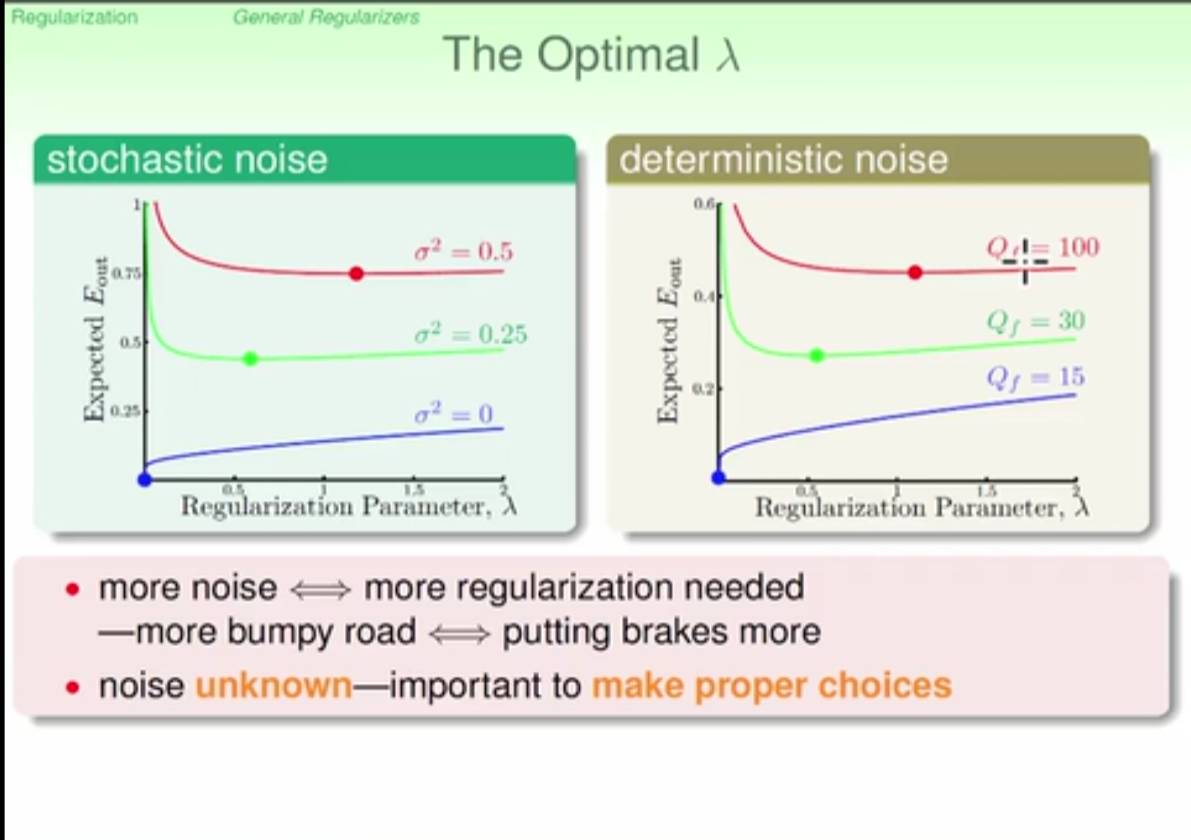
if noise is large then more regularizer is needed
validation
there are lots of hyper-parameters to choose in model selection, all of them are still guaranteed by hoeffdings rule


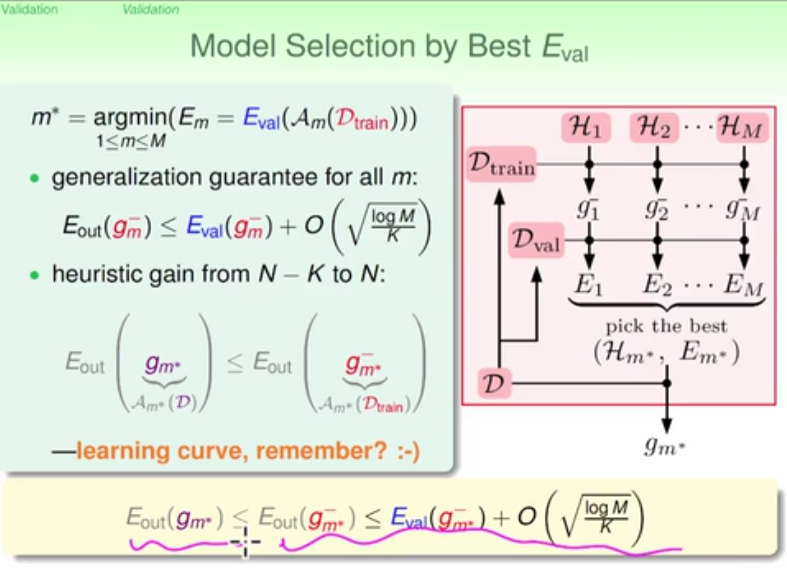
the data set should be divided into training data set and validation data set, validation data set should not be used for training purpose except for cross validation

the traing data set is used to training all modells (g), the validation set is used to select the best modell according to error level
rule of thumb to divide data set into train set and validation set
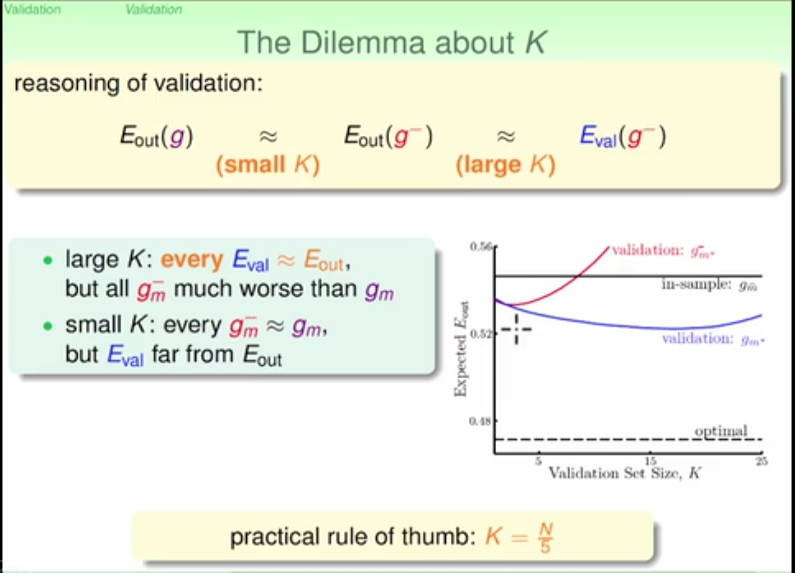
the expected error using validation estimates Eout even better than purely Ein

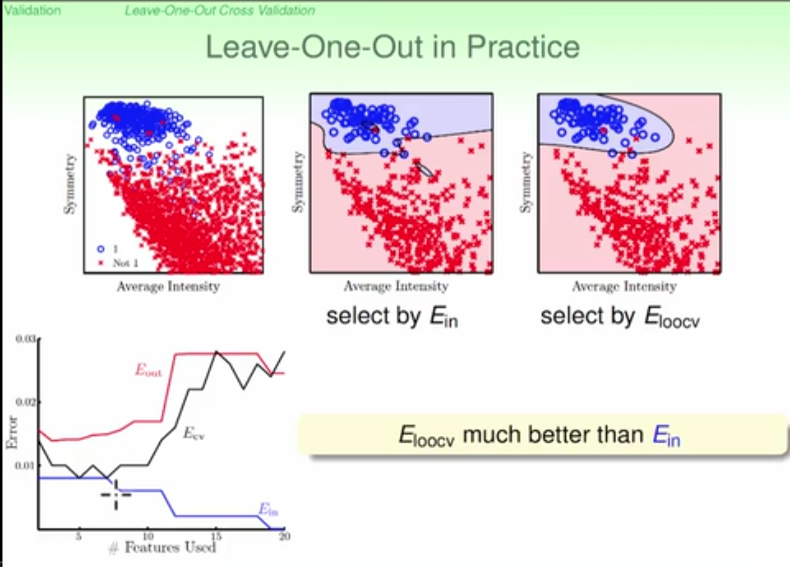
cross validation:
v-fold validation is preferred over single validation if computation allows
5 and 10 fold are good to use

some good suggestions in machine learning
start with simple model to avoid overfit

avoid biased data

avoid manual data snooping (danger of less generazation)
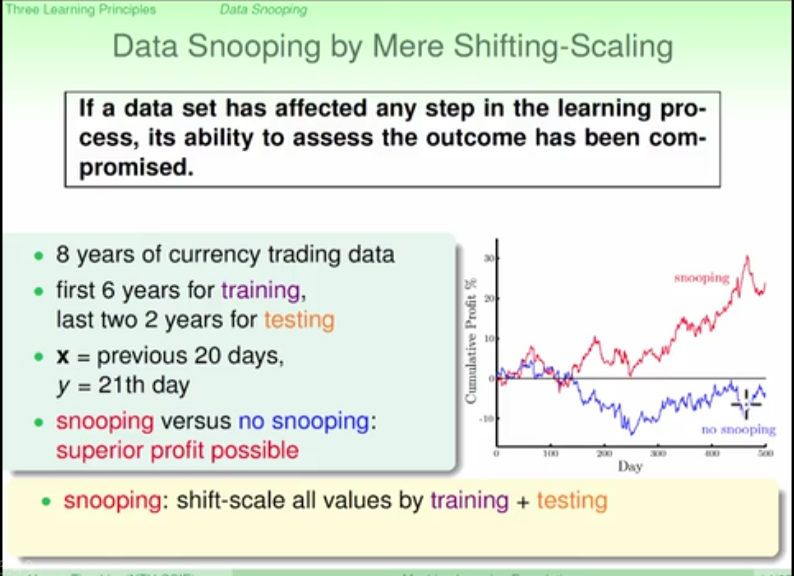


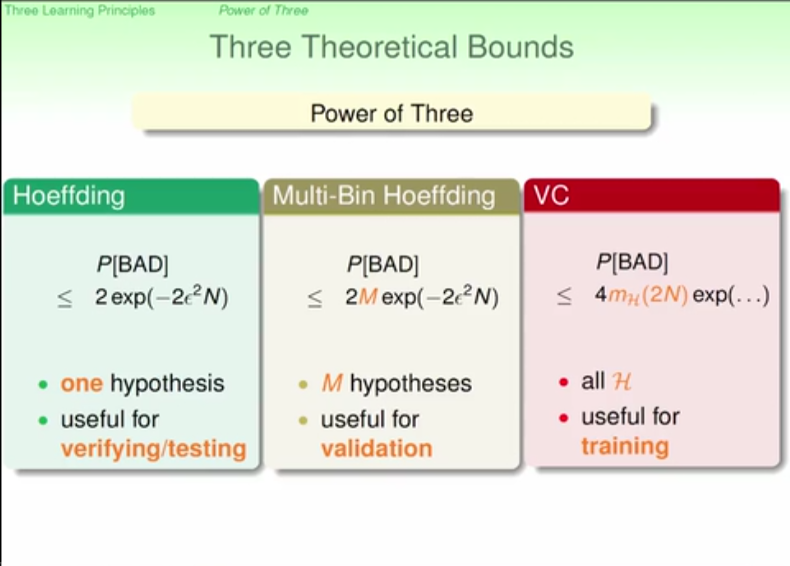
three learning principles