tensorflow Random Forest

Random forest consists of a large number of individual decision trees that operate as an ensemble (Ensemble Learning). Each individual tree in the random forest spits out a class prediction and the class with the most votes becomes our model’s prediction (see figure below).

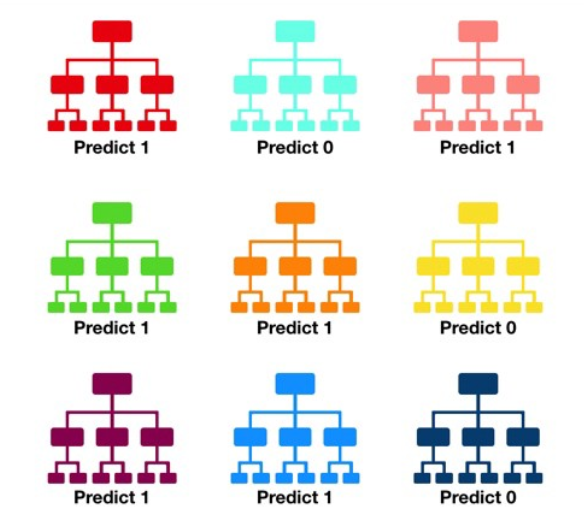
A large number of relatively uncorrelated models (trees) operating as a committee will outperform any of the individual constituent models.

decision trees

it is an supervised learning algorithm that based on if-else-then conditions.
it can be binary tree or non-binary tree

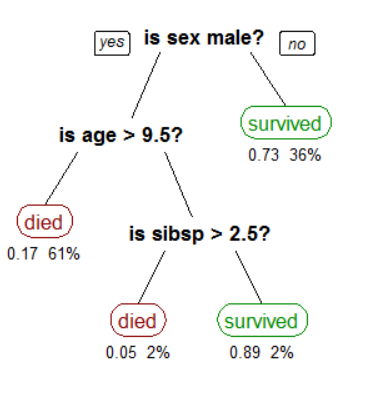
on the non-leaf node is test of attribute, each branch is the output of this test.
on the leaf nodes are classes to be classified
the decision process starts from the root node, test on the attribute node, and outputs to the corresponding branch until leaf node. the leaf node is the result of the decision tree. the growth of the tree stops when the max. depth or min. dataset size is reached. The final class is determined based on the predicted majority class in the dataset

CART (Classification and Regression Tree)

dataset will be splitted based on an attribute and an attribute threshold value. Every attribute and its threshold will be evalued with cost function. Wenn the best split attribute is found, it will be used as the next node in decision tree

cost function

regression: Sum Squared Error

classificatioin: Gini Cost Function(0: best –>1: worst) proportion=count(class_value)/count(rows) gini_index=sum(proportion*(1-proportion))

  def gini_index(groups, class_values):
      gini=0.0
      for class_value in class_values:
          for group in groups:
              size=len(groups)
              if size==0: 
                  continue
              proportion=[row[-1] for row in group].count(class_value)/float(size)
      gini+=(proportion*(1.0-proportion))                 
      return gini

process of random forest

randomly select N samples from the whole N with replacement
randomly select m attributes from the whole attributes M (m«M), the attribute to form the selection node should be selected with algorithm such as conditional entropy and information gain
every node in the selection tree should repeat step 2 until no split is possible any more
repeat step 1-3 to form multi selection trees (random forest)
notes
- random selecting N sameple with replacement and random selecting m features from M features, so that less over-fitting
- node splitting without pruning because random sampling can guarantee no overfitting

Bagging and Boosting

Bagging selects sample with replacement; Boosting does not change traing data set, only the weight of each sample changes
weight of sample in Bagging is equal; Boosting adjusts weight according to error rate (more error, more weight)
prediction weights equal in Bagging; less error prediction weights more in Boosting
parallel computing in Bagging is possible but not in Boosting

variants

Bagging+selection trees= random forest
Adaboost+selection trees=lifting trees
Gradient Boosting + selection trees=GBDT